I selected an activity presented by Ali and Colin that creatively illustrated binary numbers using concentric circles, incorporating coloring and arithmetic. Initially, I found the concept of binary numbers confusing, but it became intriguing to witness how Ali and Colin transformed this intricate idea into concentric circles, drawing inspiration from Kandinsky.
For example, in the first circle of sample 1, colors like yellow, blue, and orange represent 2+1+0, totaling 3. The next circle, displaying linen and green, corresponds to 5+3, resulting in 8. Hence, the answer is 3+8, equating to 11.
I also tried to crate an artistic piece using colors representing birthdays within our classroom community. After identifying birthdays and assigning colors to each month, I colored concentric circles, repeating layers for multiple individuals born in specific months. The final result revealed the colorful patterns.
| Lesson Plan on Addition within 20 | |
|---|---|
| Issue | Some students lack creative thinking and connections between math and art despite having fluency in adding and subtracting within 20. |
| Guiding Questions | 1. What do you see? What do you think we are learning right now? 2. What do circles and colors represent? 3. What else can we represent using colors and concentric circles? 4. What is the relationship between numbers and patterns (or colors)? |
| Integrated Learning with Outdoor Education | Let students make patterns using different materials from outside and come up with their own problems. |
| Possible Extension | Share their work with each other and collaboratively solve the problems. |
Stop 1: The Separation of Math, Science, and Art Dietiker highlights the common separation of math, science, and art, emphasizing misconceptions about the nature of science and art. This resonated with my classroom experiences, where discussions often revolve around integrating math with science and literature. For instance, our recent exploration of scientists' thinking and the scientific method involved an experiment on states of matter with baking. This activity seamlessly integrated measurement and time, leading some students to even produce procedural writing about their baking experiences.
Stop 2: Untidying Mathematical Experiences Dietiker's assertion that creating aesthetically rich mathematical classrooms requires untidying students' mathematical experiences struck a chord with me. Reflecting on my own practices, I recognize the importance of visual prompts, especially for English Language Learners in my class. Visual presentations significantly enhance their engagement and participation in solving math problems.
I found a strong connection with Dietiker's concept of math as a story. Many students express negativity towards mathematics due to its perceived difficulty. However, framing mathematical problems as stories has proven effective in cultivating a more positive attitude. When problems transform into relatable stories, students are more willing to share their thoughts and ideas verbally. Moreover, realistic and relatable "stories" prompt students to challenge themselves and engage in problem-solving. The use of manipulatives and drawing strategies further enhances their involvement in the process.
Questions Arising from the Reading:
Encouraging Student-Created Math Stories:
- How can I inspire my students to generate their own stories within the realm of mathematics? What creative prompts or approaches can be employed to nurture this storytelling aspect?
Integrated Curriculum Design:
- How can we ensure that our educational program or curriculum seamlessly integrates mathematics, art, and science? What initial steps should be taken to promote a cohesive and interconnected learning experience for students?
This reflection prompts me to consider ways to empower students as storytellers in mathematics and underscores the importance of a well-integrated curriculum that incorporates art, science, and mathematics harmoniously.


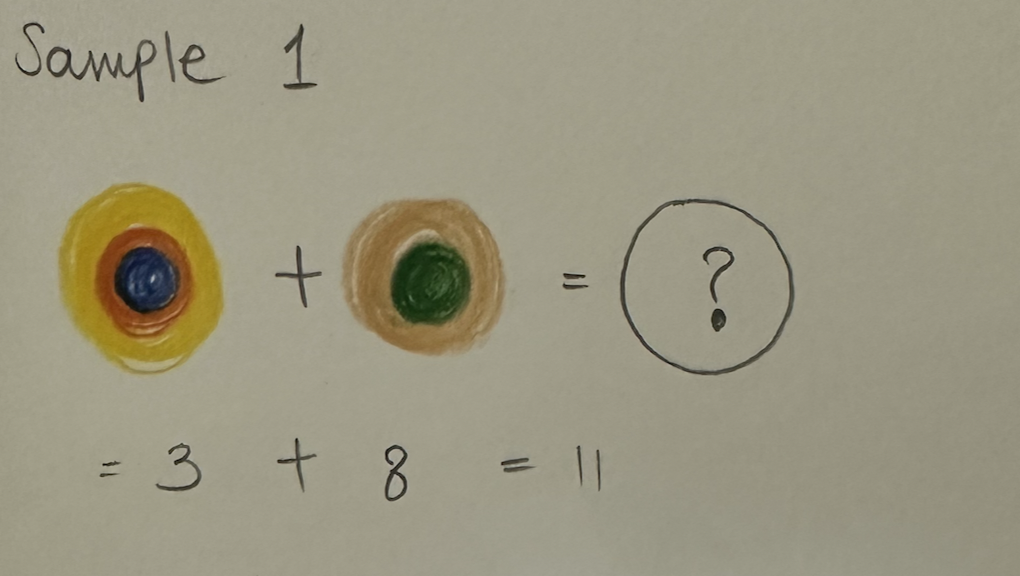





Hi Sue!
ReplyDeleteThank you for inspiring me by making the concentric circles activity accessible to younger students! So many of the lessons that we study are phenomenal but challenging for Grade 1s to access, so I always appreciate a lens toward making them useful in my classroom.
I think that connecting math with literature and stories can absolutely be done! The easiest way to start is with picture books explicitly working with mathematical concepts. It’s how I often model that math can be drawn from stories, since it’s very easy and obvious for the little ones to understand. We can often then move on to pulling math from less obvious places, like fairy tales. We also use provocations like math story tables, where students have characters and a setting and are encouraged to develop number stories (eg there are 6 fish, and now five more come! Or there are 10 fish, and a shark eats 5!) Then can then record their thinking and post their stories for others to see.